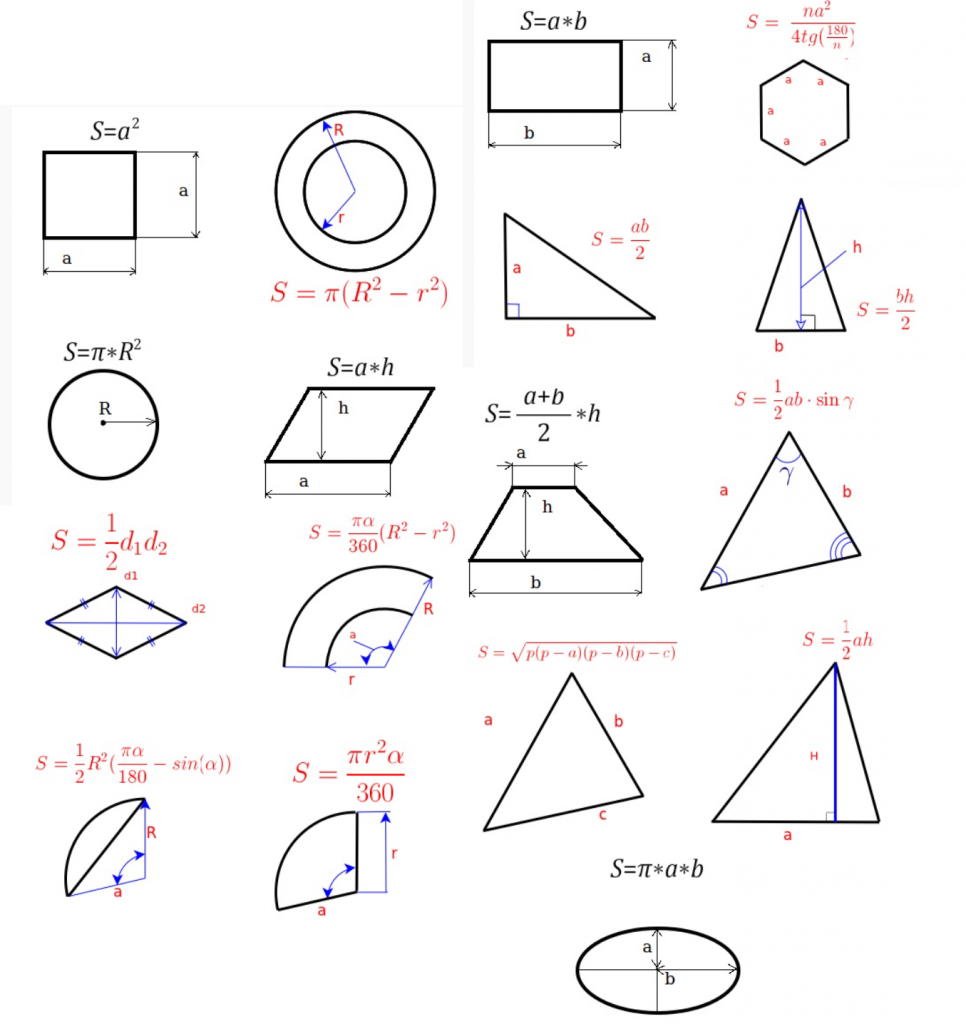
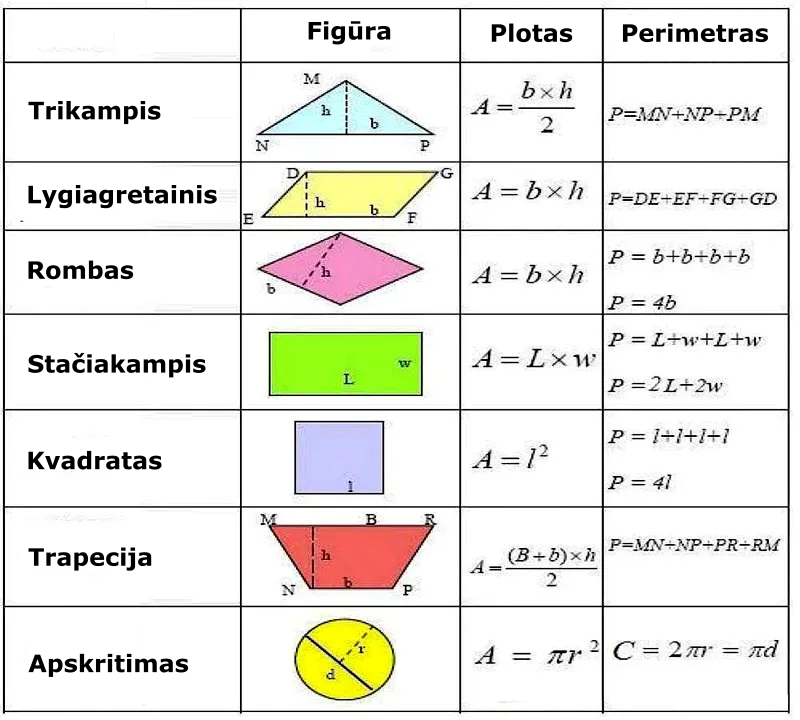
Ploto skaičiavimo formulės

Plotas – tai yra matas, kuris nusako tam tikros figūros dydį ir yra išreiškiamas kvadratiniais ploto vienetais, pvz., kvadratiniais centimetrais, kvadratiniais metrais ir t.t. Naudojantis įvairiomis formulėmis galima apskaičiuoti bet kokios figūros plotą. Jei figūra yra netaisyklingos formos, tada pirmiausia turite apskaičiuoti atskirų figūrų plotus, o tada juos sudėti.

Elektros darbai: +37065877771

Taisyklingos geometrinės formos kūno (kvadrato, stačiakampio, skritulio, rombo, lygiagretainio ir kt.) plotas apskaičiuojamas pagal geometrijos taisykles, pavyzdžiui, kvadrato plotas S = a², stačiakampio S = ab, skritulio S = πr²; čia π = 3,14.

Ploto skaičiavimo formulės. Kartais ir netaisyklingos formos kūnus galima suskirstyti į taisyklingas figūras, kurių plotą apskaičiuoti mokame.

Netaisyklingos formos figūros plotą galima išmatuoti padėjus ją ant languoto popieriaus ir nubrėžus kontūrą. Žinant vieno langelio plotą ir suskaičiavus kontūro apribotų langelių skaičių bei atsižvelgiant į tai, kad kai kuriuos langelius figūra dengia ne visiškai, randamas figūros plotas. Šitaip apskaičiuojant nedidelių figūrų plotą, geriausia jų kontūrus braižyti milimetriniame popieriuje.

Figūros plotą galima išmatuoti ir specialiu prietaisu, kuris vadinamas planimetrù (lot. planum – paviršius, plokštuma + gr. metron – matas).

Stačiakampio ploto apskaičiavimas naudojant įstrižainės ilgį:

Kadangi stačiakampį sudaro du vienodo dydžio statūs trikampiai, tai norint rasti stačiakampio plotą galima pasinaudoti Pitagoro teorema. Ši teorema – tai yra formulė, leidžianti surasti trečiąją stačiojo trikampio kraštinę, jei yra žinomos dviejų kraštinių reikšmės. Pitagoro teorema: a² + b² = c², kur a ir b – tai yra trikampio kraštinės, o c – tai įžambinė arba ilgiausia trikampio kraštinė. Pavyzdžiui: kraštinė a yra lygi 6 cm, o įžambinė c lygi 10 cm. Žinodami šiuos dydžius galima lengvai rasti kraštinę a, sustatant skaičius į formulę:

a² + b² = c²

6² + b² = 10²

36 + b² = 100

b² = 100 – 36

b² = 64

b = 8 cm

Dabar žinodami abi stačiakampio kraštines galime apskaičiuoti jo plotą: S = a * b = 6 * 8 = 48 cm². Taigi, mūsų pavyzdyje stačiakampio plotas yra lygus 48. Kadangi kraštinių ilgiai buvo žymimi centimetrais, tai ir stačiakampio plotas bus žymimas kvadratiniais centimetrais.

Kvadrato ploto apskaičiavimas naudojant įstrižainę:

Kvadrato ploto apskaičiavimo formulė, kai yra žinomas kvadrato įstrižainės ilgis, yra tokia: S = d² / 2, kur d – tai kvadrato įstrižainė. Pavyzdžiui, turime kvadratą, kurio įstrižainė yra lygi 6 cm. Žinodami šį dydį galima lengvai rasti kvadrato plotą, sustatant skaičius į formulę: S = d² / 2 = 6² / 2 = 36 / 2 = 18 cm². Taigi, mūsų pavyzdyje kvadrato plotas yra lygus 18. Kadangi įstrižainės ilgis buvo žymimas centimetrais, tai ir kvadrato plotas bus žymimas kvadratiniais centimetrais.

Apskritimo ploto apskaičiavimas naudojant spindulį:

Apskritimo spindulys – tai yra atstumas nuo bet kurio apskritimo krašto taško iki jo centro. Spindulys yra lygus pusei apskritimo skersmens ilgio. Ploto formulė, naudojant jo spindulį, yra tokia: S = πr², kur r – tai apskritimo spindulys, o π – tai pastovus dydis. Jo reikšmė yra lygi 3,14. Pavyzdžiui, norime apskaičiuoti apskritimo plotą, kurio spindulys yra 4 cm. Žinodami šį dydį, galime sustatyti skaičius į formulę: S = πr² = π * 4² = 3,14 * 16 = 50,24 cm². Taigi, mūsų pavyzdyje apskritimo plotas yra lygus 50,24. O kadangi spindulio ilgis buvo žymimas centimetrais, tai ir apskritimo plotas bus žymimas kvadratiniais centimetrais.

Apskritimo ploto apskaičiavimas naudojant skersmenį:

Apskritimo skersmuo – tai apskritimo tiesė, kuri eina per apskritimo centrą nuo vieno krašto iki kito. Skersmuo yra lygus apskritimo spinduliui padaugintam iš dviejų. Jis yra apskaičiuojamas pagal tokią formulę: d = 2 * r, kur r – tai apskritimo spindulys. Pavyzdžiui, norime apskaičiuoti apskritimo plotą, kurio skersmuo yra 8 cm. Norint rasti apskritimo spindulį, turime skersmenį padalinti iš dviejų, naudodami tokią formulę: r = d / 2 = 8 / 2 = 4 cm. Taigi, apskritimo spindulys yra lygus 4 cm. Dabar žinodami apskritimo spindulį, galime surašyti duomenis į apskritimo ploto apskaičiavimo formulę: S = πr² = π * 4² = 3,14 * 16 = 50,24 cm². Taigi, mūsų pavyzdyje apskritimo plotas yra lygus 50,24, o kadangi skersmens ilgis buvo žymimas centimetrais, tai ir apskritimo plotas bus žymimas kvadratiniais centimetrais.

Ploto skaičiavimo formulės (statyba) RU

Cilindro tūris ir paviršaus plotas

Rotacinis cilindras yra kūnas, kurį sudaro du lygiagrečiai pagrindai ir paviršius. Paviršius ir pagrindas yra lygiagretūs ir pagrindą sudaro skritulys.

Formulės

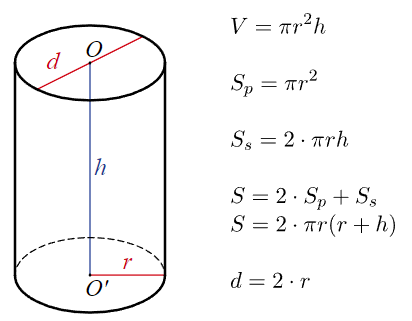
Cilindro tūris ir paviršaus plotas
V – tūris
S – paviršaus plotas
Sp – pagrindo plotas
Ss – šoninis plotas
r – spindulys
d – skersmuo
h – aukštis
O, O’ – centras

ELEKTRA. 1. Nuolatinė elektros srovė

1.1. Elektros srovė ir jos stipris / 8

1.2. Elektrinė varža. Omo dėsnis grandinės daliai / 12

1.3. Elektrinės grandinės. Nuoseklusis ir lygiagretusis laidininkų jungimas / 16

1.4. Mišrusis laidininkų jungimas / 23

1.5. Elektros srovės stiprio ir įtampos matavimas / 30

1.6. Nuolatinės elektros srovės šaltiniai. Elektrovara / 33

1.7. Omo dėsnis uždarajai grandinei / 37

1.8. Omo dėsnio uždarajai grandinei taikymas / 41

1.9. Elektros srovės darbas ir galia / 46

1.10. Buityje ir technikoje naudojami srovės šaltiniai / 51

1.11. Skyriaus „Nuolatinė elektros srovė” apibendrinimas / 56

Magnetinis laukas

2.1. Magnetinio lauko šaltiniai / 62

2.2. Magnetinės linijos. Magnetinės indukcijos vektorius / 66

2.3. Ampero jėga / 71

2.4. Nuolatinės elektros srovės variklis. Elektros matavimo prietaisai / 75

2.5. Lorenco jėga / 79

2.6. Medžiagų magnetinės savybės / 84

2.7. Laukų poveikis gyviesiems organizmams / 88

2.8. Skyriaus „Magnetinis laukas” apibendrinimas / 91

Elektros srovė įvairiose terpėse

3.1. Elektroninis metalų laidumas / 96

3.2. Elektros srovė puslaidininkiuose / 99

3.3. Puslaidininkinė sandūra. Puslaidininkiniai prietaisai / 104

3.4. Tranzistorius / 110

3.5. Elektros srovė vakuume / 113

3.6. Elektros srovė skysčiuose / 118

3.7. Elektros srovė dujose / 123

3.8. Elektros išlydis gamtoje ir technikoje / 128

3.9. Skyriaus „Elektros srovė įvairiose terpėse” apibendrinimas / 131

Elektromagnetinė indukcija

4.1. Elektromagnetinė indukcija. Magnetinis srautas /136

4.2. Indukuotosios srovės kryptis / 140

4.3. Elektromagnetinės indukcijos dėsnis / 143

4.4. Sūkurinis elektrinis laukas / 145

4.5. Judančiame laidininke indukuota elektrovara / 148

4.6. Saviindukcija. Magnetinio lauko energija / 152

4.7. Transformatorius / 155

4.8. Elektromagnetinė indukcija technikoje ir buityje / 158

4.9. Skyriaus „Elektromagnetinė indukcija” apibendrinimas /161

Elektromagnetiniai virpesiai

5.1. Laisvieji elektromagnetiniai virpesiai. Virpesių kontūras

5.2. Elektros krūvio ir srovės stiprio harmoniniai virpesiai

5.3. Priverstiniai elektromagnetiniai virpesiai

5.4. Kintamosios srovės grandinės aktyvioji varža

5.5. Ritė kintamosios srovės grandinėje

5.6. Kondensatorius kintamosios srovės grandinėje

5.7. Rezonansas kintamosios srovės grandinėje

5.8. Kintamosios srovės generatorius

5.9. Elektros energijos gamyba ir perdavimas

5.10. Elektros energetikos raida Lietuvoje

5.11. Skyriaus „Elektromagnetiniai virpesiai” apibendrinimas

Elektromagnetinės bangos

6.1. Elektromagnetinės bangos, jų spinduliavimas

6.2. Elektromagnetinių bangų skalė

6.3. Radijo ryšys. Elektroninis generatorius

6.4. Radijo ryšio principai. Radijo imtuvas

6.5. Radijo bangų ir mikrobangų taikymas ryšio priemonėse

6.6. Skaitmeninės ryšio sistemos

6.7. Skyriaus „Elektromagnetinės bangos” apibendrinimas