Nuolatinės srovės grandinės pagrindinės sąvokos ir dėsniai
Elektros srovė – kryptingas elektros krūvių judėjimas. Dar kitaip įvardijamas kaip, kryptingas laisvųjų elektringųjų dalelių judėjimas. Srovę galima paskaičiuoti pagal formulę:
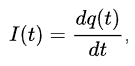
čia dq -mažas krūvio pokytis, dt – laiko pokytis (laikant abu pokyčius pakankamai mažais kad krūvį q būtų galima laikyti pastoviu). Elektros srovė grandine teka iš teigiamojo elemento poliaus neigiamojo link. Ją nešančios dalelės juda šia kryptimi jei jų elektros krūvis teigiamas. Metaluose srovę perduoda neigiamą krūvį turintys elektronai kurie juda priešinga kryptimi.
Elektros srovės tankis – skaliarinis dydis, lygus elektros krūviui, kuris praeina pro laidininko skerspjūvio plotą per laiko vienetą. Sąvoką įvedė Georgas Omas 1827 m.[1]
Momentinis srovės stipris – laidininko skerspjūviu pratekančio krūvio išvestinė laiko atžvilgiu.
Elektrinė įtampa apibūdina darbą, kurį atlieka (arba gali atlikti) elektros krūvis tekėdamas grandine. Žinodami grandine pratekėjusį elektros krūvį q ir atliktą darbą A, galime apskaičiuoti įtampą:
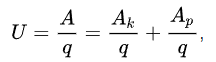
Ak – kuloninių jėgų atliktas darbas.
Ap – pašalinių jėgų atliktas darbas.
U – elektrinė įtampa. Kitas dažnai pasitaikantis žymėjimas raide V (dažniausiai ne Europos šalys).
Elektrinio lauko potencialas
Elektrinę įtampą galima apibūdinti kaip potencialo verčių pradiniame ir galiniame taške skirtumą.
Elektrinio lauko potencialas – fizikinis dydis, lygus elektriniame lauke esančio krūvio potencinės energijos ir krūvio santykiui.

kur

– elektrinio lauko potencialas;
W – elektrinio lauko potencinė energija;
q – krūvis;
r – atstumas tarp taškinių krūvių;
E – elektrinio lauko stipris;
Pratęsti pildymą….
Nuolatinė srovė – tai srovė, kuri laiko bėgyje nekeičia savo krypties.
Paprasčiausią elektros grandinę sudaro 3 elementų grupės:
- šaltiniai,
- energijos perdavimo elementai
- imtuvai
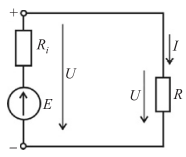 | Paprasčiausia nuolatinės srovės grandinė: E – šaltinis; Ri – šaltinio vidaus varža; R – imtuvas. |
Esant uždarai grandinei, ja teka srovė I (A), o ant atskirų elementų yra tam tikro didumo įtampa U (V).
Labai svarbu elektrinius dydžius žymėti laikantis sutartinių teigiamų krypčių sistemos (pav. aukščiau), kad būtų teisingai užrašyti daugelis elektrotechnikos dėsnių.
Grandinės srovės, įtampos ir varžos tarpusavio priklausomybę nusako Omo dėsnis. Visai grandinei jis užrašomas taip:
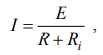 | visai grandinei |
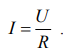 | bet kuriai grandinės daliai |
Grandinėje gali būti įjungta keletas šaltinių ir imtuvų. Tiek vienų, tiek kitų jungimas būna nuoseklus, lygiagretus ir mišrus.
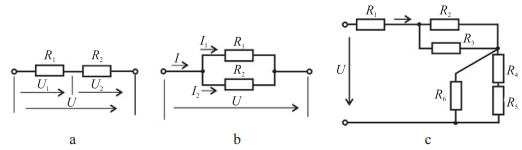 | Elementų jungimo būdai: a – nuoseklus; b – lygiagretus; c – mišrus |
Skaičiuojant grandinės nuosekliai ar lygiagrečiai sujungtus elementus, juos galima pakeisti vienu ekvivalentiniu.
Keičiant nuosekliai sujungtus elementus ekvivalentiniu, jo varža apskaičiuojama taip:
RE = R1+R2+R3+…+Rn.
Keisdami lygiagrečiai sujungtus elementus ekvivalentiniu, jo varžą apskaičiuojame iš formulės:
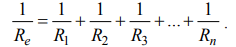
Pravartu atsiminti dviejų lygiagrečiai sujungtų varžų ekvivalentinės varžos formulę:

Bet kuriam grandinės mazgui galioja I Kirchhofo dėsnis: elektrinės grandinės mazgo srovių algebrinė suma lygi nuliui:
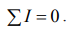
Teigiamomis laikome sroves, ištekančias iš mazgo, o neigiamomis – įtekančias į mazgą.
Bet kuriam grandinės kontūrui galioja II Kirchhofo dėsnis: kontūre veikiančių elektrovarų suma lygi įtampos kritimų kontūro varžose algebrinei sumai:

Norint naudotis šiuo dėsniu reikia žinoti srovių kryptis grandinės
šakose ir pasirinkti kontūro apėjimo kryptį. Elektrovaros ir įtampų
kritimai rašomi su teigiamu ženklu, kai laisvai pasirinkta kontūro
apėjimo kryptis sutampa su jų kryptimi. Priešingu atveju šie lygties
nariai rašomi su neigiamu ženklu.
Energetiniu požiūriu elektros grandinė arba atskiri jos elementai
charakterizuojami galia:
P=UI=I2R,W.
Bet kurioje grandinėje šaltinių atiduodama galia yra lygi imtuvuose sunaudojamų galių sumai:
∑Ps = ∑Pi; ∑EI = ∑RI2. (lygtis vadinama galių balanso lygtimi)
Jei srovė šaltinyje teka priešinga kryptimi nei jo elektrovaros kryptis, sumuojant šaltinių galias tokio šaltinio galia imama su neigiamu ženklu.
Elektrinių grandinių darbo režimai
Bet kokioje grandinėje galimi 4 darbo režimai:
- Tuščiosios veikos darbo režimas. Jis bus tuomet, kai srovė grandinėje lygi nuliui. Dažniausia tai pasiekiama jungikliu nutraukiant grandinę.
- Vardinis darbo režimas. Jis būna tuomet, kai bet kuriuo grandinės elementu teka srovė ar ant jo galų yra tokia įtampa arba jame išsiskiria tokia galia, kuriai šis elementas apskaičiuotas.
Vardiniai dydžiai žymimi indeksu N: IN, UN, PN. - Trumpojo jungimo režimas bus tuomet, kai išorinė grandinės
varža taps lygi nuliui. Srovė šio režimo metu priklauso nuo likusios grandinės varžos (šaltinio, laidų, prietaisų). Jei ši varža nedidelė, trumpojo jungimo srovė gali daug kartų viršyti vardinę elementų srovę. Todėl šis režimas laikomas avariniu. - Suderintas darbo režimas būna tuomet, kai išorinės grandinės
varža lygi likusios grandinės varžai. Šiam režimui būdinga tai,
kad jungiamaisiais laidais perduodama pati didžiausia galia.
Elektros energijos perdavimas vartotojams
Elektros energija vartotojams perduodama dvilaidėmis linijomis
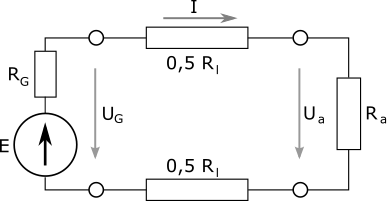 | Elektros energijos perdavimas vartotojams |
Generatoriaus gnybtų įtampa: UG = E – RGI, čia RGI – įtampos kritimas generatoriaus vidaus varžoje.
Mažėjant imtuvo varžai, srovė grandinėje didėja, didėja RGI, o įtampa ant generatoriaus gnybtų UG mažėja. Šiuolaikiniuose tinkluose šaltinių vidaus varža daug kartų mažesnė už išorinės grandinės varžą. Todėl įtampos kritimo šaltinio vidaus varžoje dažnai neįvertiname ir laikome, kad UG ≈ E .
Kai generatorius su imtuvu sujungtas energijos perdavimo linija, tekant apkrovos srovei laidais, turinčiais varžą, linijoje prarandama dalis įtampos Ud = RlI . Dėl to įtampa, tenkanti imtuvui Ua, būna mažesnė negu generatoriaus įtampa UG dydžiu Ud :
Ua = UG – Ud = UG – RlI.
Linijos laidų varžą apskaičiuojame iš formulės:
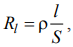 | čia p-santykinė laidininko varža, 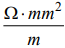 ; ; l-laido ilgis, m; S-skerspjūvio plotas, mm2. |
Tekant srovei laidais, juose susidaro galios nuostoliai:
Pd = RlI2 .
Tuomet šaltinio atiduodama galia bus lygi imtuvo galiai plius galios nuostoliai laiduose Ps = Pa + Pd. Taigi iš šaltinio pareikalaujama galia bus didesnė nei atiduodama imtuvui.
Linijos naudingumo koeficientą galima apskaičiuoti taip:

Šaltinis: „Elektrotechnikos pagrindai” Valentinas ZAVECKAS

RU kalba pagalbinė medžiaga (puikiai paaiškina):
Fizika 8 klasei 🙂 Amžius gyvenk, amžius mokykis ir kvailiu mirsi… iš patarlių…

